0450. Delete Node in a BST

https://leetcode.com/problems/delete-node-in-a-bst

Description

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.

2. If the node is found, delete the node.

Follow up: Can you solve it with time complexity O(height of tree)?

Example 1:

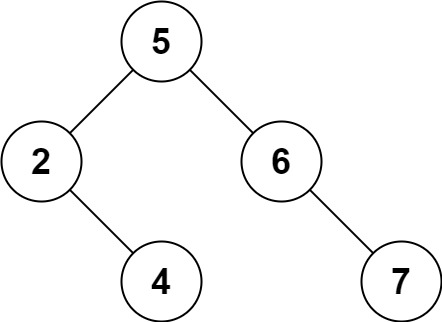
**Input:** root = [5,3,6,2,4,null,7], key = 3
**Output:** [5,4,6,2,null,null,7]
**Explanation:** Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.
![](https://assets.leetcode.com/uploads/2020/09/04/del_node_supp.jpg)

Example 2:

**Input:** root = [5,3,6,2,4,null,7], key = 0
**Output:** [5,3,6,2,4,null,7]
**Explanation:** The tree does not contain a node with value = 0.

Example 3:

**Input:** root = [], key = 0
**Output:** []

Constraints:

• The number of nodes in the tree is in the range [0, 104].

• -105 <= Node.val <= 105

• Each node has a unique value.

• root is a valid binary search tree.

• -105 <= key <= 105

ac

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        // exit
        if (root == null) return root;

        if (key < root.val) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        } else {
            if (root.left == null && root.right == null) {
                return null;
            } else if (root.left == null) {
                return root.right;
            } else if (root.right == null) {
                return root.left;
            } else {
                root.val = minValue(root.right);
                root.right = deleteNode(root.right, root.val);
            }
        }

        return root;        
    }

    private int minValue(TreeNode root) {
        while (root.left != null) {
            root = root.left;
        }
        return root.val;
    }
}

/*
find that value: 1) return null if left/right null; 2) return left if right null; 3) return right if left null; 4) find minValue in right, upate in root.val, delete minValue in right, return root.
*/